Mathematical constants by continued fraction representation
This is a list of mathematical constants sorted by their representations as continued fractions.
Continued fractions with more than 20 known terms have been truncated, with an ellipsis to show that they continue. Rational numbers have two continued fractions; the version in this list is the shorter one. Decimal representations are rounded or padded to 10 places if the values are known.
[*]Although some of the symbols in the leftmost column are displayed in black due to math markup peculiarities, all are clickable and link to the respective constant's page.
| Symbol[*] | Member of | decimal | Continued fraction | Notes |
|---|---|---|---|---|
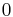 |
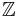 |
0.00000 00000 | [0; ] | |
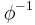 |
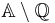 |
0.61803 39887 | [0; 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, …] | First positive irrational number in the list. |
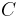 |
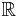 |
0.64341 05463 | [0; 1, 1, 1, 4, 9, 169, 16641, 639988804, 177227652025317609, 72589906463585427805281295977816196, …] | Continued fraction truncated at 10 terms due to large size. |
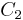 |
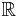 |
0.66016 18158 | [0; 1, 1, 1, 16, 2, 2, 2, 2, 1, 18, 2, 2, 11, 1, 1, 2, 4, 1, 16, 3, …] | Hardy–Littlewood's twin prime constant. Presumed irrational, but not proved. |
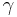 |
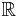 |
0.57721 56649 | [0; 1, 1, 2, 1, 2, 1, 4, 3, 13, 5, 1, 1, 8, 1, 2, 4, 1, 1, 40, 1, …] | Presumed irrational, but not proved. |
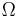 |
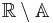 |
0.56714 32904 | [0; 1, 1, 3, 4, 2, 10, 4, 1, 1, 1, 1, 2, 7, 306, 1, 5, 1, 2, 1, 5, …] | |
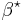 |
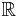 |
0.70258 | [0; 1, 2, 2, 1, 3, 5, 1, 2, 6, 1, 1, 5, …] | Value only known to 5 decimal places. |
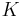 |
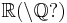 |
0.76422 36535 | [0; 1, 3, 4, 6, 1, 15, 1, 2, 2, 3, 1, 23, 3, 1, 1, 3, 1, 1, 7, 2, …] | May have been proven irrational. |
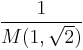 |
 |
0.83462 68417 | [0; 1, 5, 21, 3, 4, 14, 1, 1, 1, 1, 1, 3, 1, 15, 1, 3, 8, 36, 1, 2, …] | Gauss's constant |
 |
 |
0.87058 83800 | [0; 1, 6, 1, 2, 1, 2, 956, 8, 1, 1, 1, 23, …] | Brun's prime quadruplet constant. Estimated value; 99% confidence interval ± 0.00000 00005. |
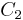 |
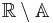 |
0.86224 01259 | [0; 1, 6, 3, 1, 6, 5, 3, 3, 1, 6, 4, 1, 3, 298, 1, 6, 1, 1, 3, 285, …] | Base 2 Champernowne constant. The binary expansion is 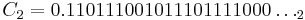 |
 |
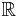 |
0.91596 55942 | [0; 1, 10, 1, 8, 1, 88, 4, 1, 1, 7, 22, 1, 2, 3, 26, 1, 11, 1, 10, 1, …] | Presumed irrational, but not proved. |
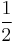 |
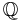 |
0.50000 00000 | [0; 2] | |
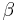 |
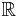 |
0.28016 94990 | [0; 3, 1, 1, 3, 9, 6, 3, 1, 3, 13, 1, 16, 3, 3, 4, …] | Presumed irrational, but not proved. |
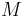 |
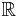 |
0.26149 72128 | [0; 3, 1, 4, 1, 2, 5, 2, 1, 1, 1, 1, 13, 4, 2, 4, 2, 1, 33, 296, 2, …] | Presumed irrational, but not proved. |
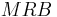 |
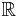 |
0.18785 96424 | [0; 5, 3, 10, 1, 1, 4, 1, 1, 1, 1, 9, 1, 1, 12, 2, 17, 2, 2, 1, 1, …] | |
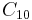 |
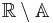 |
0.12345 67891 | [0; 8, 9, 1, 149083, 1, 1, 1, 4, 1, 1, 1, 3, 4, 1, 1, 1, 15, 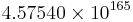 , 6, 1, …] , 6, 1, …] |
Base 10 Champernowne constant. Champernowne constants in any base exhibit sporadic large numbers; the 40th term in 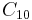 has 2504 digits. has 2504 digits. |
 |
 |
1.00000 00000 | [1; ] | |
 |
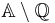 |
1.61803 39887 | [1; 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, …] | |
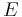 |
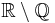 |
1.60669 51524 | [1; 1, 1, 1, 1, 5, 2, 1, 2, 29, 4, 1, 2, 2, 2, 2, 6, 1, 7, 1, 6, …] | Not known whether algebraic or transcendental. |
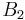 |
 |
1.90216 05823 | [1; 1, 9, 4, 1, 1, 8, 3, 4, 7, 1, 3, 3, 1, 2, 1, 1, 12, 4, 2, 1, …] | Brun's twin prime constant. Estimated value; best bounds 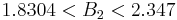 . . |
 |
 |
1.45607 49485 | [1; 2, 5, 5, 4, 1, 1, 18, 1, 1, 1, 1, 1, 2, 13, 3, 1, 2, 4, 16, 4,, …] | |
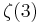 |
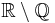 |
1.20205 69032 | [1; 4, 1, 18, 1, 1, 1, 4, 1, 9, 9, 2, 1, 1, 1, 2, 7, 1, 1, 7, 11, …] | |
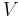 |
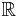 |
1.13198 82488 | [1; 7, 1, 1, 2, 1, 3, 2, 1, 2, 1, 17, 1, 1, 2, 1, 2, 4, 1, 2, …] | Viswanath's constant. Apparently, Eric Weisstein calculated this constant to be approximately 1.13215 06911 with Mathematica. |
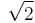 |
 |
1.41421 35624 | [1; 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, …] | |
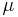 |
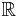 |
1.45136 92349 | [1; 2, 4, 1, 1, 1, 3, 1, 1, 1, 2, 47, 2, 4, 1, 12, 1, 1, 2, 2, 1, …] | Presumed irrational, but not proved. |
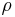 |
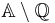 |
1.32471 95724 | [1; 3, 12, 1, 1, 3, 2, 3, 2, 4, 2, 141, 80, 2, 5, 1, 2, 8, 2, 1, 1, …] | |
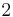 |
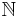 |
2.00000 00000 | [2; ] | |
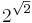 |
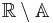 |
2.66514 41426 | [2; 1, 1, 1, 72, 3, 4, 1, 3, 2, 1, 1, 1, 14, 1, 2, 1, 1, 3, 1, 3, …] | |
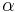 |
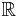 |
2.50290 78751 | [2; 1, 1, 85, 2, 8, 1, 10, 16, 3, 8, 9, 2, 1, 40, 1, 2, 3, 2, 2, 1, …] | |
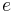 |
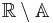 |
2.71828 18285 | [2; 1, 2, 1, 1, 4, 1, 1, 6, 1, 1, 8, 1, 1, 10, 1, 1, 12, 1, 1, 14, …] | |
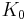 |
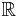 |
2.68545 20011 | [2; 1, 2, 5, 1, 1, 2, 1, 1, 3, 10, 2, 1, 3, 2, 24, 1, 3, 2, 3, 1, …] | |
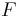 |
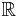 |
2.80777 02420 | [2; 1, 4, 4, 1, 18, 5, 1, 3, 4, 1, 5, 3, 6, 1, 1, 1, 5, 1, 1, 1, …] | |
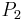 |
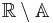 |
2.29558 71494 | [2; 3, 2, 1, 1, 1, 1, 3, 3, 1, 1, 4, 2, 3, 2, 7, 1, 6, 1, 8, 7, …] | |
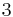 |
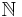 |
3.00000 00000 | [3; ] | |
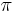 |
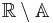 |
3.14159 26536 | [3; 7, 15, 1, 292, 1, 1, 1, 2, 1, 3, 1, 14, 2, 1, 1, 2, 2, 2, 2, 1, …] | |
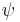 |
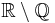 |
3.35988 56662 | [3; 2, 1, 3, 1, 1, 13, 2, 3, 3, 2, 1, 1, 6, 3, 2, 4, 362, 2, 4, 8, …] | |
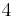 |
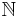 |
4.00000 00000 | [4; ] | |
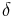 |
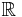 |
4.66920 16091 | [4; 1, 2, 43, 2, 163, 2, 3, 1, 1, 2, 5, 1, 2, 3, 80, 2, 5, 2, 1, 1, …] | |
 |
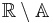 |
23.14069 26328 | [23; 7, 9, 3, 1, 1, 591, 2, 9, 1, 2, 34, 1, 16, 1, 30, 1, 1, 4, 1, 2, …] | Gelfond's constant. Can also be expressed as 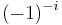 ; from this form, it is transcendental due to the Gelfond–Schneider theorem. ; from this form, it is transcendental due to the Gelfond–Schneider theorem. |